Как вырастить филогенетический лес?

Что за наука такая — филогенетика?

Ученые-филогенетики ищут родственные связи между группами живых организмов (как на межвидовом, так и на внутривидовом уровне), стремятся смоделировать, каким образом проходил эволюционный процесс на Земле, и создать эволюционную классификацию.

Родственные взаимоотношения между организмами и группами организмов можно установить на основе нуклеотидных или аминокислотных последовательностей. В качестве математической методологии для этого используют инструменты филогенетического анализа. Самый распространенный способ иллюстрации результатов такого анализа — филогенетическое дерево.

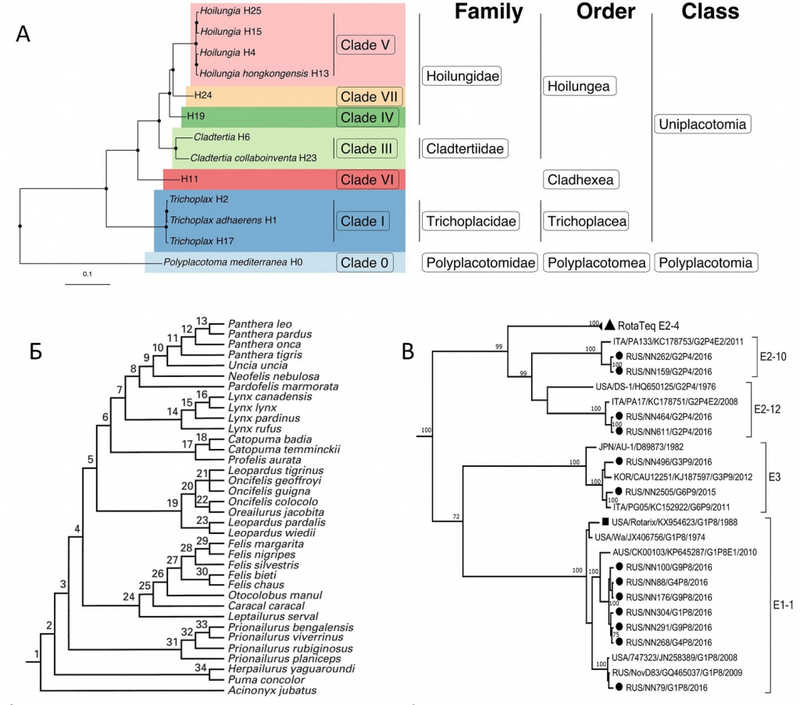 Использование филогенетических деревьев на разных таксономических уровнях. А – филогенетическое дерево, отражающее таксономию  типа Пластинчатые (Placozoa); Б – филогенетическое дерево, включающее разные виды  семейства кошачьих (Felidae); В – филогенетическое дерево, отражающее разные генотипы  внутри одного вида — ротавируса А.

Что такое филогенетическое дерево и где у него листья?

Филогенетическое дерево представляет собой ориентированный граф — структуру, состоящую из точек (вершин) и путей между ними (ребер), причем последние имеют направления.

На филогенетическом дереве принято выделять ветви, узлы и корень.

Узлы — это вершины графа. Терминальные, или внешние узлы (terminal nodes) отражают положение организмов, по которым у нас есть данные (нуклеотидные или аминокислотные последовательности). Эти структуры также называются оперативными таксономическими единицами (ОТЕ или OTU), терминальными таксонами или листьями (leafs). Они могут быть представлены вымершими или ныне живущими особями. Внутренние узлы (internal nodes) — их гипотетические предки. Ветви (branches) представляют собой связи между узлами и являются ребрами графа. Корень (root) — это гипотетический предок всех организмов, составляющих дерево. Общее расположение корня, ветвей, узлов, листьев относительно друг друга называется топологией дерева.

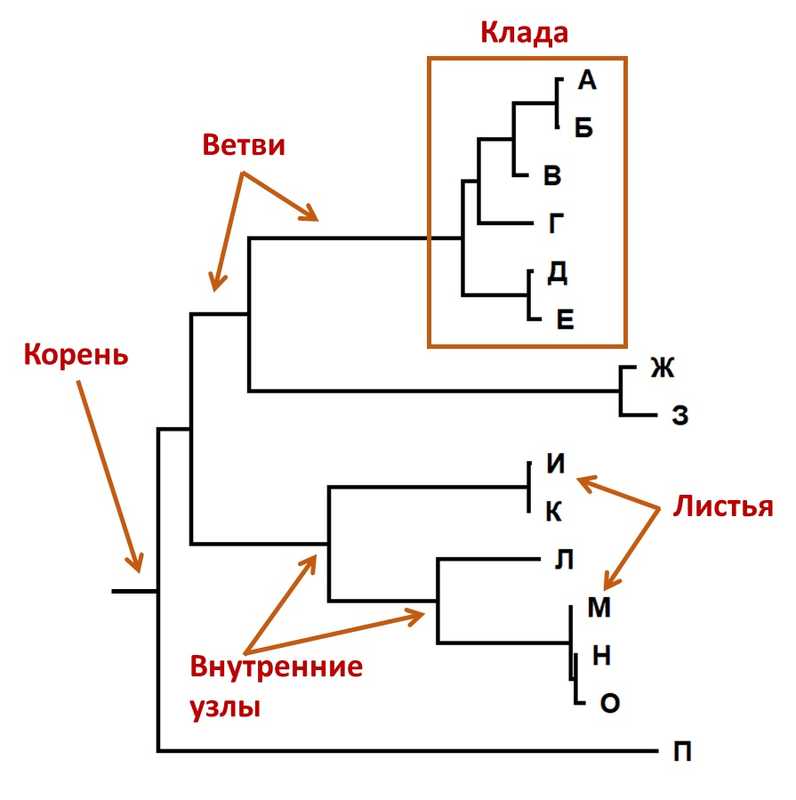 Основные элементы филогенетического дерева

В зависимости от выбора исследователя деревья могут быть укорененными (иметь корень) или неукорененными (не иметь корня). Они служат для решения разных задач. Деревья с корнем показывают направление эволюции в анализируемой группе организмов — порядок их ответвления от предков, а деревья без корня служат только для иллюстрации родственных связей между ними.

Каждый внутренний узел является последним общим предком (the most recent common ancestor, tMRCA) всех отделившихся от него последовательностей (расположены правее). Например, узел 3 — последний общий предок для последовательностей А–Г, а узел 5 — для последовательностей А–Е. Внутренние узлы отражают момент, после которого произошло расхождение двух линий (дивергенция, дихотомия, бифуркация), и далее их эволюция шла независимо друг от друга.

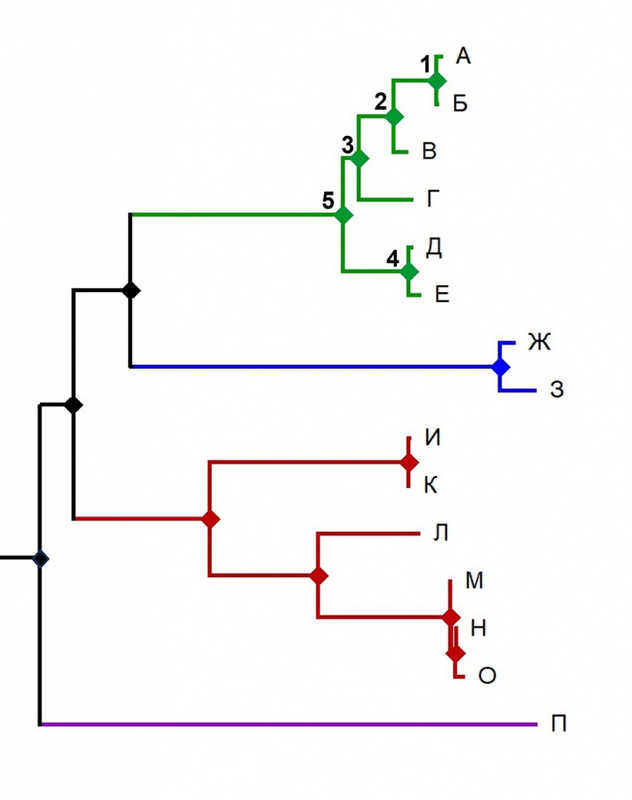 Взаимоотношения элементов на филогенетическом дереве (пояснения в тексте)

Группа двух или более организмов, которая включает общего предка и всех его потомков, называется клада (clade). Для обозначения группы последовательностей также могут употребляться термины кластер и линия. Например, последовательности А–Е образуют общий кластер (зеленый), а последовательности Д, Е, Ж, З – нет, несмотря на то, что располагаются на дереве близко друг от друга.

Зеленая и синяя клады А–Е и Ж–З являются сестринскими — у них имеется предок, общий только для этих двух групп и ни для каких иных. Вместе сестринские клады образуют монофилетическую группу.

Понятно, что полифилетической называют группу, которая включает узлы, происходящие от разных предков, но объединенные по какому-то другому признаку, например, морфологическому. А парафилетическая — группа, включающая потомков одного общего предка, но не всех; иначе говоря, такая группа, из которой исключены одна или несколько монофилетических групп. Парафилетической группой являются, например, рыбы: четвероногие позвоночные происходят от того же общего предка, но к рыбам традиционно не относятся (хотя, строго говоря, все четвероногие — специализированные рыбы).

Клада, отмеченная красным и включающая последовательности И–О, — базальная (basal) по отношению к ним, так как ее эволюционная линия отделилась от корня раньше. Похожим понятием является внешняя группа (outgroup). Это такая последовательность, которая ответвилась от общего предка заведомо (но минимально!) раньше разделения интересующих нас клад. Обычно этот термин употребляют в контексте анализа всего дерева, а в качестве внешней группы берут представителей другого генотипа/вида/семейства. Например, фиолетовая ветвь П представляет собой внешнюю группу для зеленой, синей и красной клад, включающих листья А-О. (Термин «базальная клада» относится скорее к тому, как люди описывают взаимное расположение ветвей, а термин outgroup — скорее технический, он используется при построении дерева, о чем поговорим дальше.)

Графическое представление дерева может быть самым разным, например, прямоугольным, круговым или радиальным.

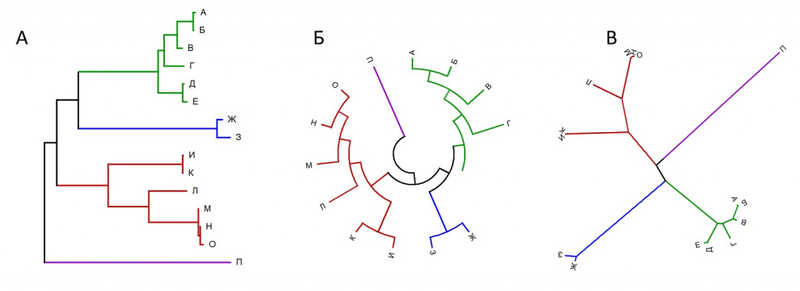 Разные типы представления филогенетических деревьев, иллюстрирующие родственные связи в одной и той же группе организмов: прямоугольное (А), круговое (Б) и радиальное (В)

По отношению к построенным деревьям ученые используют такие термины, как дендрограмма, кладограмма или филограмма.

Дендрограмма — самый общий из них, который обозначает просто схематическое изображение филогенетического дерева. Кладограмма отражает только топологию (взаимное расположение клад), длина ветвей не несет информации. На филограмме, напротив, длина ветвей пропорциональна эволюционному расстоянию между узлами — внизу всегда указан масштаб, отражающий, например, число мутаций. Значение имеют только длины горизонтальных линий, а вертикальные просто облегчают зрительное восприятие дерева. Хронограмма — частный случай филограммы, где длина ветвей соответствует эволюционному времени.

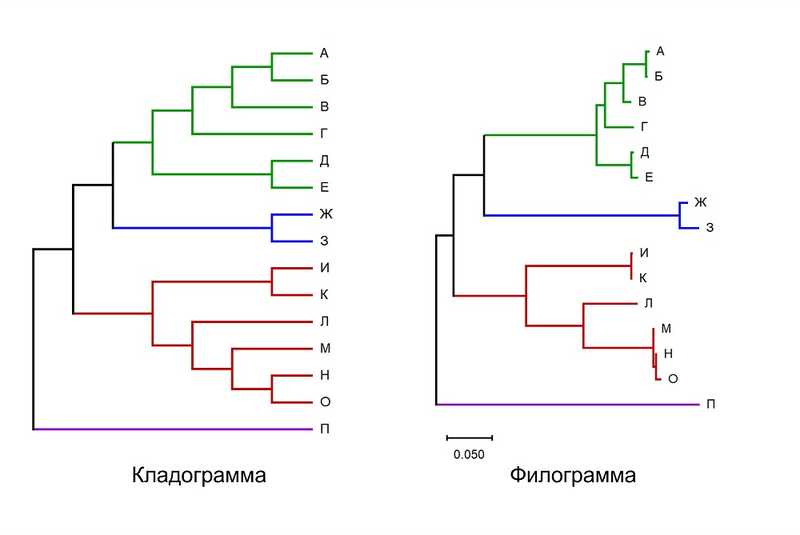 Разница между дендрограммой и филограммой

Самое главное, что следует помнить: филогенетическое дерево — это только модель, гипотеза. Она может отражать реальные события, с высокой или не очень высокой вероятностью, а может и вовсе не иметь к ним отношения.

А как сделать так, чтобы дерево надежно отражало эволюционные события?

В основе удачного дерева всегда лежит хорошая выборка нуклеотидных последовательностей. При ее составлении сначала нужно прояснить для себя некоторые вопросы. Самое главное: какова цель нашего анализа и какие результаты мы планируем получить? От этого зависит объем предполагаемой выборки и ее состав.

Другие вопросы не менее важны. С какими организмами мы будем сравнивать интересующие нас последовательности? Какие референсные (общеизвестные, хорошо изученные, прототипные) последовательности используют другие исследователи? А что мы возьмем в качестве внешней группы, чтобы упорядочить интересующие нас ветви? А какой длины наша последовательность? Мы возьмем отдельный ген или только его фрагмент? А какие вычислительные мощности нам доступны? Возможно, быстрее и проще будет проанализировать гены хлоропластов, если нас интересуют растения, или митохондриальные гены, если мы изучаем животных? Или мы — вирусологи, и можем позволить себе роскошь анализировать полные геномы? Ответы на все эти вопросы впоследствии позволят сделать корректные выводы. На самом старте лучше всего посмотреть последние статьи по интересующей теме и постараться повторить то, что делают коллеги, добавив свои сиквенсы.

Например, китайские и американские ученые решали такую сложную задачу, как реконструкция эволюционной истории целого подсемейства Нолиновые (Nolinoideae) семейства Спаржевые. Они взяли в анализ 129 нуклеотидных последовательностей, составленных из 68 объединенных пластидных белок-кодирующих генов общей длиной 65 859 п. н. В выборку взяли пластомы 80 видов из шести ветвей подсемейства Нолиновые, а также представителей остальных шести подсемейств Спаржевых и пяти других семейств порядка Спаржецветные. Это помогло им отразить разнообразие клад внутри порядка. В качестве внешней группы, для того, чтобы упорядочить все эти ветви на дереве друг относительно друга, они взяли пластомы шести видов родственного порядка Лилиецветные. Такая обширная выборка позволила им не только построить достоверное филогенетическое дерево, но и рассчитать время возникновения основных клад внутри подсемейства Нолиновые.

А перед учеными из Китая, которые получили полный геном хлоропластов спиреи монгольской (Spiraea mongolica Maxim), такой большой задачи не стояло. Им нужно было только описать этот геном и определить филогенетическое положение вида. Они добавили в выборку последовательности 28 родственных видов семейства Розовые и двух видов Бобовых в качестве внешней группы. Такая выборка была достаточной и позволила подтвердить, что спирея монгольская группируется среди представителей семейства Розовые, и установить ее близкое родство со спиреей Блюме (Spirea blumei G.Don).

Не для всех задач нужно собирать большую выборку или анализировать длинный фрагмент последовательности. Например, для изучения четырех особей власоглавов (Trichuris sp.), обнаруженных в кишечнике двугорбых верблюдов, испанские ученые секвенировали три митохондриальных (cox1, cob и rrnL) и два рибосомальных гена (ITS1 и ITS2), длина которых варьировала от 291 до 1114 п.н. Число нуклеотидных последовательностей в выборках для каждого гена было тоже невелико — от 17 (ген rrnL) до 45 (ген cox1). Кроме этого, специалисты использовали такой подход, как объединение последовательностей нескольких генов (только рибосомальных, только митохондриальных или всех) в одну. Например, в случае объединения всех генов каждой особи у них получилась выборка из 15 последовательностей (для этих четырех особей и других, взятых из GenBank) длиной 2728 п.н. Это помогло исследователям уточнить топологию деревьев и прояснить филогенетические отношения паразитов внутри рода Trichuris, поражающих млекопитающих разных видов.

Как только мы определились с ответами на основные вопросы, можно начать собирать последовательности в выборку, находя их в GenBank по номерам из заинтересовавших нас статей, либо проводя поиск родственников наших сиквенсов в BLAST.

Следующий важный этап — выравнивание. Оно заключается в поиске такого взаимного расположения фрагментов последовательностей, при котором наименее измененные (консервативные) участки находятся в одном и том же положении друг относительно друга. Последовательности в выборке должны быть идеально выровнены, чем меньше пропусков — тем лучше. Собрать и выровнять последовательности можно в программах MEGA, UGENE и многих других.

Практические советы

• Убедиться, что для всех анализируемых организмов в выборку пошли последовательности одного и того же фрагмента генома, а не разных.

• Не брать в анализ сомнительные, короткие, рекомбинантные последовательности или такие, которые имеют множество вырожденных оснований или пропусков (gaps).

• Лучше вырезать блоки, содержащие много пропусков и плохо выровненные концы.

• Для начала лучше брать не более 50 последовательностей.

• Использовать внешнюю группу (outgroup).

• Обязательно визуально проверить качество выравнивания.

Как смоделировать эволюцию на уровне нуклеотидов?

Следующий этап после выравнивания нуклеотидных (или аминокислотных) последовательностей — определение эволюционных дистанций между ними. Эволюционная дистанция показывает различие последовательностей, определяемое числом и качеством отличий нуклеотидов (аминокислот).

В самом простом случае для установления дистанции могут использоваться наблюдаемые различия — нуклеотиды (аминокислоты), неодинаковые у двух интересующих нас последовательностей. Такое различие называется p-дистанцией (p-distance). Это пропорция числа неодинаковых нуклеотидов (аминокислот) у двух последовательностей в пересчете на длину фрагмента последовательностей в выравнивании. Она может быть выражена в долях единицы либо в процентах. Например, если две последовательности имеют три неодинаковых нуклеотида, а их длина 30 нуклеотидов, то p-дистанция между ними составляет 3/30х100%=10%. Эту дистанцию можно понимать и как среднюю частоту замены каждого нуклеотида в последовательности. Так, средняя наблюдаемая частота замены каждого нуклеотида в приведенном примере составляет 10%.

Однако использование р-дистанции, основанной только на наблюдаемых различиях, не подходит для установления истинных эволюционных дистанций по следующим причинам:

1. Одно наблюдаемое различие между двумя последовательностями не означает, что оно было результатом только одной замены — могли произойти множественные замены (несколько последовательных мутаций) в этой позиции. Более того, отсутствие различий в каких-либо позициях не означает, что замен в них не было — могли произойти обратные замены или одинаковые замены в обеих сравниваемых последовательностях. Получается, что р-дистанция недооценивает истинное число замен. В реальной эволюции их было больше, чем мы наблюдаем.

2. Известно, что разные типы замен имеют разную вероятность. Вероятность транзиций (замен пуринового основания на пуриновое, или пиримидинового на пиримидиновое) в общем случае выше вероятности трансверсий (замен пуринового основания на пиримидиновое или наоборот).

3. Вероятности (скорости, если говорить о ходе эволюции) замен в разных позициях последовательностей также могут различаться.

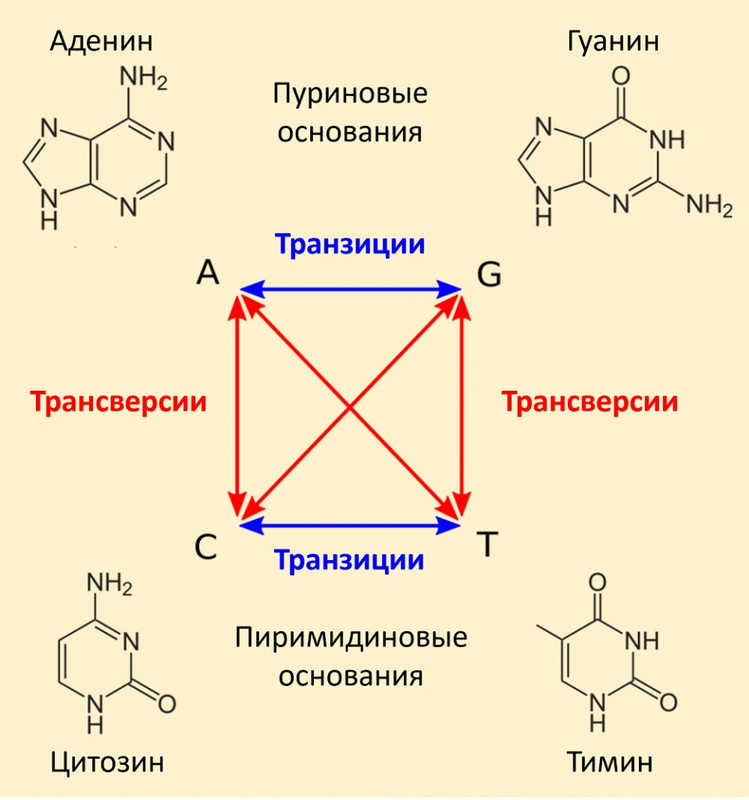 Возможные типы замен нуклеотидов. Транзиции происходят чаще, чем трансверсии

Истинную эволюционную дистанцию мы можем лишь оценить, а не узнать наверняка. Для этого используют расчетные дистанции, основанные на различных представлениях о частоте нуклеотидных замен. Математически эти представления описываются в различных эволюционных моделях (evolutionary model). В основном они рассматривают эволюцию нуклеотидных последовательностей, а не аминокислотных. Следует отметить, что наличие нуклеотидной замены является результатом комплексного процесса — возникновения мутации и ее последующего отбора, закрепления. Мутации, несовместимые с жизнью особи, не закрепляются в ходе отбора, нейтральные, не влияющие на фенотип, накапливаются из поколения в поколения, а полезные мутации отбором поддерживаются, хотя с точки зрения химии нуклеиновых кислот эти три типа ничем не различаются. Однако при описании с помощью моделей эволюции этот процесс рассматривается как единое целое.

Модель Джукса-Кантора (Jukes-Cantor model) — исторически первая, предложена в 1969 году. Сокращенно называется JC69 — по начальным буквам фамилий авторов и году публикации их статьи. Модель исходит из того, что вероятность (частота) замены любого нуклеотида на любой другой за единицу времени одинакова и равняется a — то есть является однопараметрической.

Модель Кимуры (Kimura model, K80, двухпараметрическая модель Кимуры, K2P). Учитывает экспериментальные данные, согласно которым частота транзиций выше частоты трансверсий. Для каждого нуклеотида возможна одна транзиция и две трансверсии. Модель предполагает, что транзиция любого нуклеотида в рассматриваемой позиции за единицу времени происходит с частотой α, а частота каждой из двух возможных трансверсий — β. Таким образом, модель Кимуры является двухпараметрической.

Существуют множество других моделей: Тадзимы–Нея (Tajima-Nei model, TN84), Хасэгавы–Кишино–Яно (Hasegawa–Kishino–Yano model, HKY85), трехпараметрическая модель Тамуры (Tamura model, T92, T3P), Тамуры–Нея (Tamura-Nei model, TN93) и другие. Они различаются тем, что по-разному учитывают 1) π — частоту замен на любой из четырех нуклеотидов (без учета исходного), 2) частоту переходов между пуриновыми и пиримидиновыми нуклеотидами (транзиции, Ts, и трансверсии, Tv), 3) другие аспекты, например, влияние суммарного содержания нуклеотидов G и C (GC-содержание).

Сравнение некоторых моделей по набору учитываемых параметров

Рассмотренные модели подразумевают, что частоты замен являются одинаковыми для всех позиций рассматриваемых последовательностей. Но такое предположение может и не выполняться. Поэтому при расчете эволюционных дистанций можно учесть не только разную частоту разных типов замен, но и разную вероятность замен в разных позициях. Например, частота замен в участках, кодирующих антигенные детерминанты, будет выше, чем в участках, не подвергающихся иммунному давлению – закрепление таких замен будет занимать меньше времени. А участок, который кодирует активный центр жизненно важного фермента, будет изменяться медленнее, если вообще будет.

Считается, что частота замен в разных позициях варьирует согласно гамма-распределению (это такое непрерывное распределение вероятностей, которое используется для моделирования времени между событиями, при этом параметр формы a определяет среднее время, в течение которого обычно происходит событие, а параметр масштаба q — вариацию этого времени). Этот момент можно учесть в любой из моделей – такая возможность обозначается как «+G» в названии модели (например, TN93+G). Это допущение иногда расширяют, предполагая, что какая-то часть позиций в последовательности вообще не изменялась в процессе эволюции. Такие сайты называются инвариантными, а допущение обозначается как «+I» в названии модели (например, TN93+I). Можно использовать оба этих предположения сразу (TN93+G+I).

Практические советы

• Подбирать оптимальную модель нужно для каждого нового выравнивания.

• Можно протестировать несколько моделей и, если все деревья получились хорошими, выбрать ту, которая проще.

• Но лучше использовать Байесовский информационный критерий (Bayesian Information Criterion, BIC) или информационный критерий Акаике (Akaike Information Criterion, AIC). Чем их значения меньше — тем лучше модель описывает данные. Проще всего посчитать их в программе MEGA. Перфекционисты могут использовать отдельную программу — jModelTest, которая берет в сравнение большее число моделей.

Так как же вырастить дерево?

Существуют много методов построения филогенетических деревьев, которые можно условно разделить на две группы: алгоритмические и оптимизирующие. Первые просто используют заранее сформированный алгоритм для построения, а вторые ищут дерево, оптимальное с точки зрения некоторой заданной функции, часто путем перебора всех вариантов. Разберем три таких подхода подробнее.

Метод присоединения ближайших соседей (Neighbor-Joining, NJ). Это алгоритмический метод, и принцип его работы состоит в поэтапном поиске пар соседних последовательностей таким образом, чтобы минимизировать общую длину ветвей дерева. За основу алгоритм берет полностью неразрешенное дерево — оно имеет форму звезды, таксоны не связаны между собой, и все отходят от общего центра. Сначала алгоритм ищет такую пару последовательностей, при объединении которых длина всех ветвей дерева будет минимальна. Для этого он случайным образом берет два листа, объединяет их в группу, а все остальные при этом считает другой группой. Далее он строит матрицу дистанций между ними. А потом повторяет все то же самое, группируя попарно все остальные листья, и выбирает такую версию, в которой расстояния получились минимальными. Из выбранной пары таксонов формируется новый узел, и весь цикл повторяется до тех пор, пока поэтапно не будут присоединены все последовательности.

Этот метод построения филогенетического дерева — один из самых быстрых, но не очень точный. Его, например, использовали уже упоминавшиеся китайские ученые, чтобы определить филогенетическое положение полного генома хлоропластов спиреи монгольской среди представителей семейства Rosaceae — для решения их задачи подходил простой метод.

 Пример филогенетического дерева, построенного методом присоединения ближайших соседей

Метод максимального правдоподобия (Maximum likelihood, ML). Это оптимизирующий метод, и он подбирает изначально неизвестные параметры эволюционной модели так, чтобы максимизировать функцию правдоподобия. Другими словами, этот метод работает как бы наоборот, не выстраивает дерево из имеющихся данных, а ищет такую топологию дерева, при которой вероятность получить наше выравнивание нуклеотидных (аминокислотных) последовательностей максимальна. Этот метод демонстрирует правильную топологию дерева чаще других методов, однако требует значительных вычислительных мощностей. Метод максимального правдоподобия для построения филогенетического дерева применили ученые из Франции, Испании и США, чтобы подтвердить видовую принадлежность особей иберийских кротов (Talpa occidentalis) Для этого они использовали нуклеотидные последовательности митохондриального гена цитохрома b длиной 1140 п.н.

 Пример филогенетического дерева, построенного методом максимального правдоподобия

Филогенетические деревья с помощью NJ и ML, а также других методов можно построить в программах MEGA, UGENE и других — их существует великое множество, но не все они обладают дружественным пользователю графическим интерфейсом.

Байесовский подход (Bayesian inference, BI) использует алгоритм Монте-Карло по схеме марковской цепи (Markov chain Monte Carlo approach, MCMC). Цепь Маркова — это последовательность событий или действий, где каждое новое зависит только от предыдущего. Интуитивно это можно рассматривать как случайное блуждание: алгоритм находится в определенной точке и шагает в следующее состояние, исходя из вероятности этого следующего состояния с учетом текущего. Некоторые точки он может посещать чаще, чем другие (их вероятность больше). Байесовский подход сочетает в себе элементы алгоритмических методов (для построения марковских цепей эволюционных событий) и оптимизирующих методов (для максимизации так называемых апостериорных вероятностей используемых параметров моделей и моделируемых событий). Апостериорная вероятность — условная вероятность, которая рассчитывается не только на основе исходных данных, известных на момент начала анализа, но и корректируется по ходу самого анализа, по мере появления новых данных (апостериорных), которые тоже можно применить для расчетов.

Байесовский подход позволяет выбрать статистически наиболее достоверное филогенетическое дерево из всех возможных вариантов на основании расчета вероятности существования такого дерева при условии, что имеется дополнительная информация о свойствах исследуемой популяции (например, данные о географическом происхождении и времени сбора образца). Этот подход считается наиболее продвинутым, однако требует значительного времени и (или) имеет повышенные требования к вычислительным мощностям.

Для построения деревьев с использованием байесовского подхода существуют пакет программ BEAST и опция MrBayes в программе UGENE. Классическая программа MrBayes имеет интерфейс командной строки и не подходит для новичков.

Испанские ученые определяли кротов не ради самих кротов, а ради исследования хантавирусов у насекомоядных. Наряду с ML, для решения своей основной задачи ученые использовали метод BI и построили деревья на основе S, M и L-сегментов вирусного генома. Благодаря этому они обнаружили у иберийских кротов три генетически различных хантавируса: NVAV (Nova virus), BRGV (Bruges virus) и новый вирус, получивший название ASTV (Asturia virus).

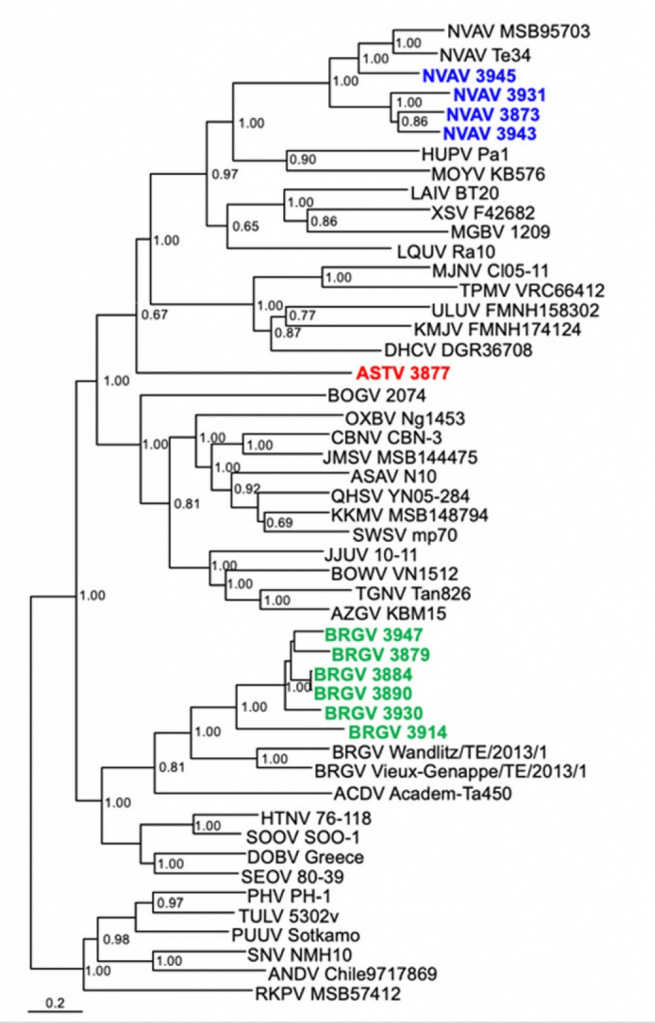 Пример филогенетического дерева, построенного с помощью байесовского подхода

Практические советы

• Метод присоединения ближайших соседей лучше использовать в ситуации, когда нужно быстро построить предварительное дерево, например, чтобы проверить, хорошая ли получилась выборка последовательностей.

• Метод максимального правдоподобия стоит использовать в ситуациях, когда нужно более точное дерево и есть достаточно времени на расчеты.

• Оптимально сначала несколько раз построить дерево методом NJ, чтобы сформировать хорошую выборку, а потом запустить рассчитываться финальное дерево методом ML.

• Байесовский подход можно попробовать в случае, когда предыдущими методами достоверное дерево получить не удалось, а в запасе есть много времени и достаточная вычислительная мощность.

• Часто в одном исследовании для построения деревьев сочетают разные подходы — ML и BI. Это позволяет получить более достоверную топологию дерева.

Как узнать, хорошее ли получилось дерево?

Важный критерий оценки филогенетического дерева — проверка надежности каждой из его ветвей. Один из самых распространенных подходов для этого — бутстреп-анализ (bootstrap analysis). Такой анализ происходит следующим образом: в выравнивании случайно выбирается одна из позиций (столбик, сформированный одной буквой из каждой последовательности) и записывается как первая для нового, генерируемого выравнивания. Затем снова случайным образом выбирается еще одна позиция и записывается как вторая. Эта процедура повторяется такое количество раз, которое соответствует длине последовательностей в нашем выравнивании, в результате формируется первая случайная выборка (псевдовыборка). Аналогично создается вторая и последующие такие выборки — исследователь сам задает их число. Обычно генерируют от 100 до 1000 случайных выборок.

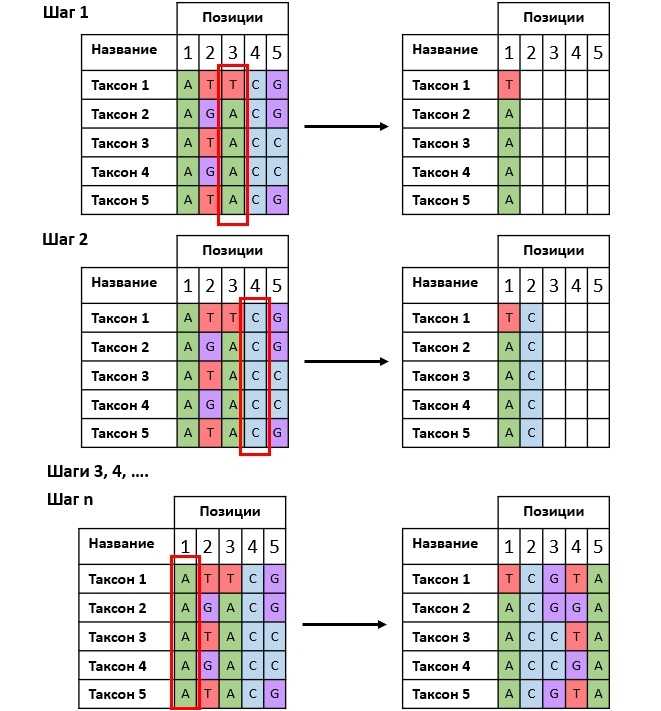 Принцип формирования случайной выборки

После этого для каждой из них строится филогенетическое дерево с использованием того же самого метода, что и то дерево, которое мы проверяем. Все деревья, построенные на основе псевдовыборок, сравнивают с анализируемым, проверяя, есть ли в них те же самые внутренние узлы. Для каждого внутреннего узла подсчитывают процент деревьев, в которых присутствует тот же самый узел, и записывают рядом с ним на дереве — это и есть значение бутстреп (bootstrap value). Это значение отражает вероятность получить такое же дерево при использовании псевдовыборок, основанных на анализируемых последовательностях. Чем надежнее дерево построено по нашему выравниванию, тем выше будут значения бутстреп для его узлов. Как правило, достоверными считают узлы, для которых это значение превышает 70, а лучше 90.

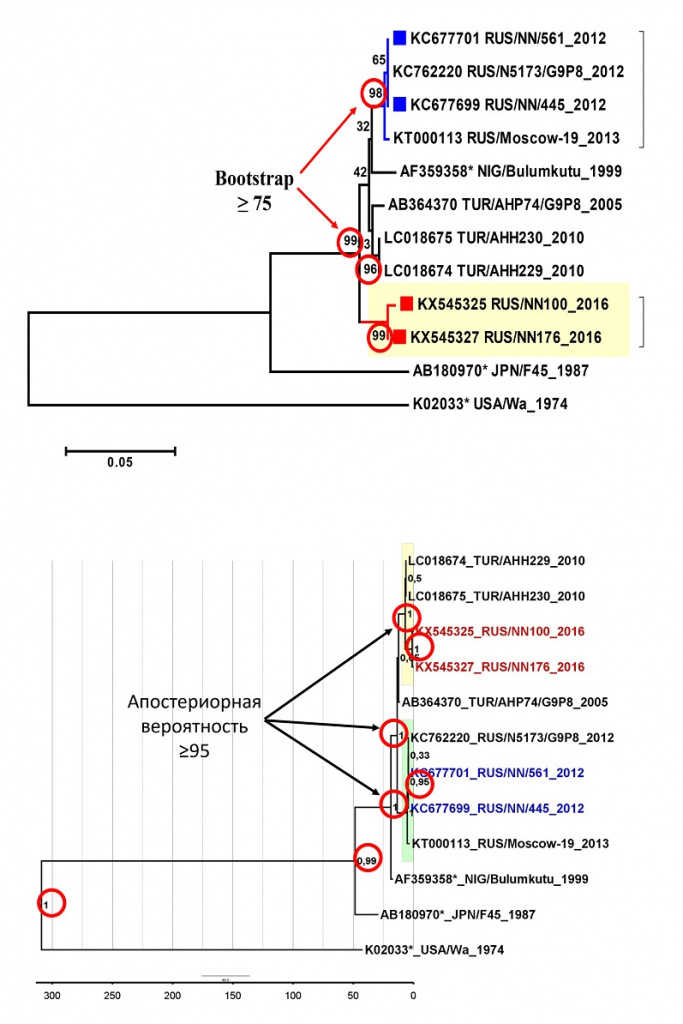 Значения бутстреп и апостериорной вероятности на филогенетических деревьях

При использовании байесовского подхода программа сразу ищет такое филогенетическое дерево, которое обладает максимальной надежностью клад (maximum clade credibility tree, MCC). Оно характеризуется максимальными апостериорными вероятностями узлов. Достоверными считаются узлы с апостериорной вероятностью более 0,95.

Как завести молекулярные часы?

Концепцию молекулярных часов (molecular clock) впервые предложили Эмиль Цукеркандль и Лайнус Полинг в 1962 году. По их предположению, скорость эволюции постоянна во времени и одинакова для всех нисходящих эволюционных линий (дочерних последовательностей), произошедших от некой одной последовательности (нуклеотидной или аминокислотной). Под скоростью эволюции подразумевается число эволюционных изменений в единицу времени, например, количество нуклеотидных замен на сайт в год. Если оно постоянно, то время расхождения двух последовательностей можно измерить количеством накопленных мутаций. Например, если дивергенция двух последовательностей, отличающихся на 2 нуклеотида, произошла 5 лет назад, то расхождение между ними и третьей последовательностью, которая отличается на 4 нуклеотида, было 10 лет назад.

Таким образом, эволюционные события в изучаемой группе могут быть (теоретически!) легко датированы. Но на практике не все так просто. Если число отличий между изучаемыми последовательностями мы можем оценить, то как измерить скорость эволюции? Ведь, как правило, последовательность их общего предка нам неизвестна.

Определение скорости эволюции называют калибровкой молекулярных часов. Необходим внешний источник информации, чтобы пересчитать относительное время расхождения ветвей в абсолютное. Одна из стратегий использует для такой калибровки информацию о возрасте самих секвенированных образцов. В этом случае датирование возможно только при наличии достаточного разброса в их возрасте. Для этого идеально подходят наборы данных быстро развивающихся таксонов, например, вирусов. Для таких расчетов используют программы BEAST или MrBayes.

Применяя такой подход, ученые из Португалии смоделировали эволюцию основных линий вируса гепатита В. Они взяли в выборку 453 частичные последовательности гена полимеразы длиной 749 п.н. от штаммов из разных стран мира, отобранных с 1963 по 2018 годы — такой разброс оказался достаточным для калибровки. По их расчетам, средняя скорость накопления мутаций у вируса гепатита В составила 9,45x10^-5 замен на сайт в год. Это значение позволило им предположить, что вирус возник примерно в 886 году, а затем разделился на две ветви. Одна из них дала начало генотипу А, а другая – генотипам D и E. Из всех изученных современных генотипов первым, вероятно, был генотип D, который появился около 1501 года и разветвился на субгенотипы D3 и D4 во второй половине XVIII века.

Ученые из Китая и США, исследовавшие филогению и эволюцию подсемейства Нолиновые, проводили калибровку молекулярных часов по-другому. Они использовали ранее рассчитанную другими исследователями информацию о временных расхождениях внутри порядка Спаржецветные. Получились следующие калибровочные точки: 116,32 млн лет назад — возраст общего предка всего порядка Спаржецветные (Asparagales), 52,09 млн лет назад — дивергенция семейств Амариллисовые (Amaryllidaceae) и Спаржевые (Asparagaceae), 49,53 млн лет — возраст общего предка семейства Спаржевые. Эти и другие точки позволили сделать выводы о времени возникновения основных клад в подсемействе Нолиновые.

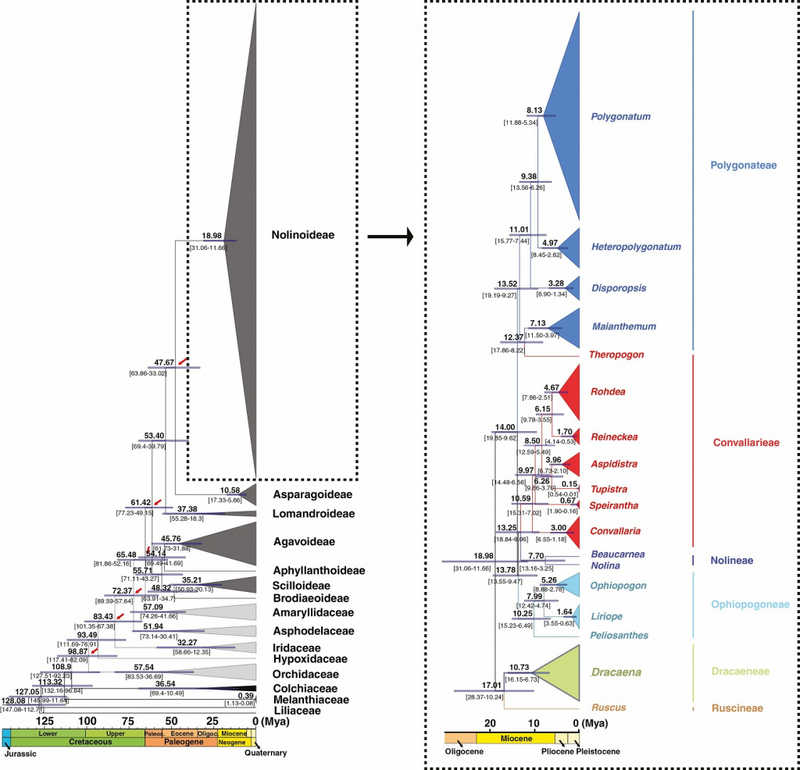 Датированное филогенетическое дерево порядка Спаржецветные. Красными стрелками отмечены калибровочные точки. Временная шкала и время дивергенции показаны в миллионах лет назад (Mya). Клады преобразованы в треугольники при редактировании дерева для улучшения зрительного восприятия, при этом ширина основания треугольника пропорциональна количеству таксонов в кладе.

Далеко ли до края филогеографии?

Основная задача филогеографии — выяснение места происхождения того или иного вида, а также путей его миграции и внедрения на новые территории. В этом случае ученые строят филогенетические деревья, объединяя генетические данные и информацию о географическом распределении популяции. Сделать такой анализ можно в BEAST. Результаты часто визуализируют в программах, позволяющих спроецировать филогенетическое дерево на карту, например SpreaD3. В качестве исходных данных используют координаты мест получения образцов либо просто населенных пунктов или стран. Далее узлы дерева преобразуются в точки на карте, а ветви — в линии.

Так, португальские ученые задались вопросом, какую роль их страна сыграла в распространении вируса гепатита В мире, и смоделировали возможные пути его заноса. По их расчетам, например, субгенотип D3 проник в Португалию через Францию около 1882 года, а затем около 1909 года был привезен в Бразилию, а также распространился в США (1882) и Испанию (1932).

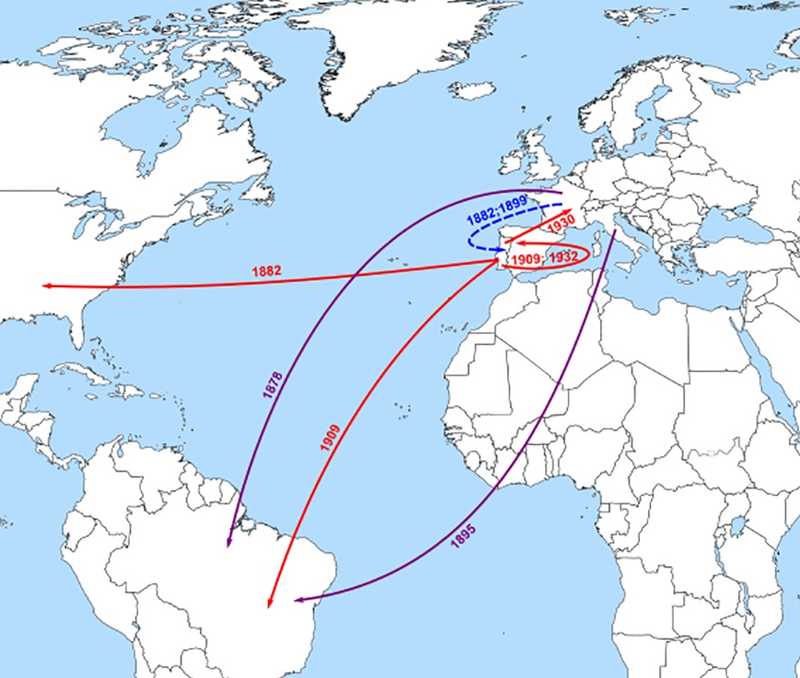 Основные пути распространения вируса гепатита В (субгенотип D3), затрагивающие Португалию

Китайские ученые выясняли, как засушливый климат в Центральной Азии и поднятие горного массива Тянь-Шань в неогене, разделившее Центральную Азию и регион Гоби, влияли на биом. Они провели филогеографическую реконструкцию пути распространения пустынного скорпиона Mesobuthus mongolicus в сочетании с моделированием экологической ниши (ENM), для чего использовали 342 последовательности гена субъединицы I митохондриальной цитохром-С-оксидазы. Согласно их расчетам, M. mongolicus представляет собой целостную линию, которая возникла в Центральной Азии около 1,36 млн лет назад. Предковая популяция постепенно расселялась из Центральной Азии на восток, через Джунгарский бассейн в регион Гоби. Два крупных события — заселение Джунгарского бассейна и южной части Гоби — произошли, вероятно, в межледниковые периоды (около 0,8 и 0,4 млн лет назад, соответственно), когда климатические условия были аналогичны современным. В эти периоды ареал распространения скорпиона был максимально широким.

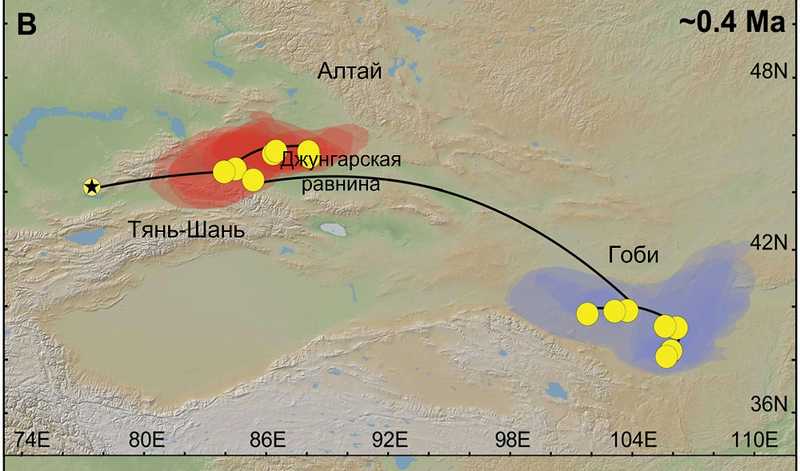 Путь расселения скорпиона Mesobuthus mongolicus из Центральной Азии в регион Гоби

Все эти сложные филогенетические моделирования сегодня доступны не только опытным специалистам или именитым ученым. Полюбопытствовать и попробовать филогеографию «на зуб» может каждый. Пандемия COVID-19 принесла большую популярность базе данных GISAID, которая прежде содержала геномы вирусов гриппа. Теперь в ней хранится более 16,5 миллионов последовательностей генома SARS-CoV-2. Функционал сайта позволяет любому желающему в интерактивном режиме не только посмотреть филогенетическое дерево с интересующими изолятами коронавируса, но и сразу же получить анимированную иллюстрацию путей их распространения на карте. В качестве примера — видеореконструкция путей заносов варианта Пирола (он же BA.2.86.1 или JN.1), наиболее распространенного в мире зимой 2023-2024 гг., из США, Франции и Великобритании на территорию России.

Филогенетический анализ позволяет решить огромное число научных задач, затрагивающих живые организмы всех царств. Однако важно помнить, что филогенетическое дерево – это всего лишь результат моделирования. Велик риск того, что оно не будет отражать эволюционную историю так точно, как нам бы хотелось. Поэтому необходимо заранее продумать, какие моменты эволюции мы хотим с его помощью проиллюстрировать, собрать корректную выборку нуклеотидных последовательностей и учесть все нюансы анализа, подходящие именно нашему набору данных. Очень важно ориентироваться во всем многообразии параметров филогенетического анализа, уметь корректно их подбирать, постоянно изучать появляющиеся программы и подходы. А еще интересоваться, как проводят такой анализ коллеги.

Литература

Tessler M. et al. Phylogenomics and the first higher taxonomy of Placozoa, an ancient and enigmatic animal phylum. Front. Ecol. Evol. 2022. DOI:  10.3389/fevo.2022.1016357

Bininda-Emonds O.R. et al. Building large trees by combining phylogenetic information: a complete phylogeny of the extant Carnivora (Mammalia). Biol Rev Camb Philos Soc. 1999 May;74(2):143-75. DOI:  10.1017/s0006323199005307

Morozova O.V. et al. Phylogenetic comparison of the VP7, VP4, VP6, and NSP4 genes of rotaviruses isolated from children in Nizhny Novgorod, Russia, 2015-2016, with cogent genes of the Rotarix and RotaTeq vaccine strains. Virus Genes. 2018 Apr;54(2):225-235. DOI:  10.1007/s11262-017-1529-9

Ji Y. et al. Phylogeny and evolution of Asparagaceae subfamily Nolinoideae: new insights from plastid phylogenomics. Annals of Botany, Volume 131, Issue 2, 1 February 2023, Pages 301–312, DOI:  10.1093/aob/mcac144

Ma Y. et al. The complete chloroplast genome of Spiraea mongolica Maxim. Mitochondrial DNA B Resour. 2021 May 12;6(5):1614-1616. DOI:  10.1080/23802359.2021.1926351

Rivero J. et al. New genetic lineage of whipworm present in Bactrian camel (Camelus bactrianus). Vet Parasitol. 2023 Mar;315:109886. DOI: 10.1016/j.vetpar.2023.109886

Gu S.H. et al. Multiple Lineages of Hantaviruses Harbored by the Iberian Mole (Talpa occidentalis) in Spain. Viruses. 2023 Jun 2;15(6):1313. DOI:  10.3390/v15061313

Marcelino R. et al. 2022. Phylogeography of hepatitis B virus: The role of Portugal in the early dissemination of HBV worldwide. PLoS ONE 17(12): e0276618. DOI:  10.1371/journal.pone.0276618

Shi C.-M. et al. Phylogeography of the desert scorpion illuminates a route out of Central Asia, Current Zoology, Volume 69, Issue 4, August 2023, Pages 442–455, DOI:  10.1093/cz/zoac061